- $x = \text{ some number}$
- $x = 3$
- $x = \frac{5+4}{3}$
- $0=0$
- We would not be able to solve
- $x = x$
|
One way to think about the expression $3(x-4)+5$ is as the set of instructions "Take a number, subtract 4, multiply by 3, and finally add 5. We can then try out our "number recipe" using several different inputs, the numbers $1, 2, \text{ and } 3.$ We received the results of $-4, -1, \text{ and } 2,$ for inputs of $1, 2, 3,$ respectively. We can take another expression $3x-7$ and do the same thing: translate it into verbal instructions and apply these instructions to several inputs. Doing so, we achieve "Take a number, multiply by 3, then subtract 7$ as well as the numerical results below. Notice that these resulting numbers are the same as the resulting numbers. This leads to a reasonable definition: equivalent expressions are expressions whose instructions give the same output for the same input. Explaining the above calculations was how I began our class discussion. I had additional comments planned, but a student's question caught me off guard, "What happens if you set two equivalent expressions equal and try to solve?" This was not the direction I had planned for the lesson, but I decided this question was worth pursuing. I wrote the equation $3(x-4)+5=3x-7$ on the board and asked the class what they thought would happen when we solved. I received a wide range of responses. By then solving this equation as a class we were involved involved in creating knowledge together. Students knew how to do the calculations, they understood the question, and they cared about the answer, because they had made hypotheses about the outcome. I think these three components will allow my class to remember the concepts much more fully, and our lively discussion was initiated by a student asking a question.
0 Comments
Leave a Reply. |
About Me
I started this blog to share my transformation from math nerd to math nerd who loves to share math with young people. I teach high school in Hanoi, Vietnam. Your comments are always welcome. Archives
May 2021
|
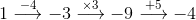
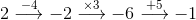
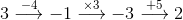
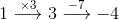

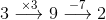
 RSS Feed
RSS Feed
