|
Some functions, like $\ln (x)$, grow to infinity very slowly. Others, like $e^x$, grow very quickly. Most functions fall somewhere in between. Armed with L'Hôpital's Rule and pre-calculus algebra skills, students were able to create a precise ordering of functions according to their rates of growth. Only afterwards, did I create this speed chart to summarize their results. (The animal additions were inspired by some student doodling.) In a second, two-day investigation, students were asked to evaluate improper integrals based on the functions whose speeds we had ranked. For each function $f$ in our ranking, they considered the integral $$\int_2 ^\infty \frac{1}{f(x)}dx,$$ trying to decide if it converges or diverges. On the first day of the investigation, students were not permitted a calculator and were able to evaluate some of the simpler integrals. On the second day, students could use a graphing calculator. By comparing integrals of unknown convergence to previously evaluated integrals, students were able to determine the convergence/divergence of all the remaining integrals. My students are so smart. They articulated their findings, "If the function is faster than $x$, that integral converges. If the function is $x$ or slower, that integral diverges." (That summary is so close to correct!) There is a relationship between a function's rate of growth and whether the corresponding integral converges!
2 Comments
Kim Eberle Wang
2/5/2015 10:12:36 pm
I like the idea of using the doodle I wonder what other math ideas can be expressed by doodling.
Reply
Leave a Reply. |
About Me
I started this blog to share my transformation from math nerd to math nerd who loves to share math with young people. I teach high school in Hanoi, Vietnam. Your comments are always welcome. Archives
May 2021
|
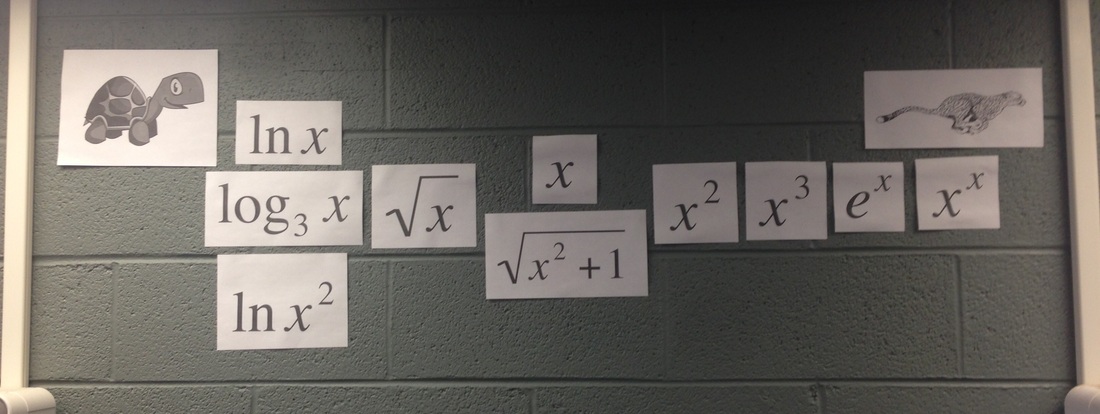
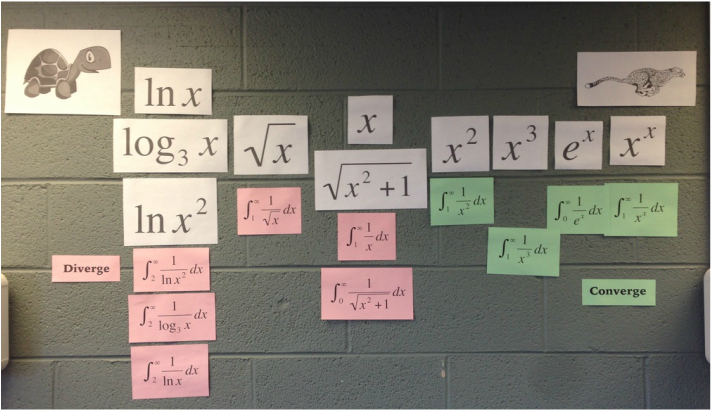
 RSS Feed
RSS Feed
