| Assignment
| Building Plans
| ||||
|
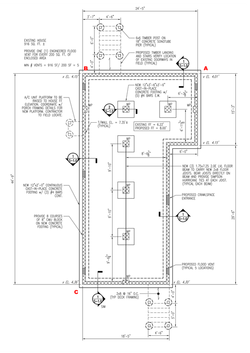
Civilizations have been using Geometry to do surveying work since ancient times. Our Geometry class decided to use an old theorem to help them lay the foundation for a new building. A friend who works in construction was generous enough to let our class use the building plans above. We took the plans out to the field to lay the "foundation" for the new construction. The Pythagorean Theorem was able to provide us with the diagonal lengths to make sure we had perfect 90° angles. Classroom Materials
0 Comments
When one solves an algebraic equation, what authority can one turn to to check the validity of the answer? Unfortunately, there is no easy answer to this question. My most recent attempt at empowering students to be their own mathematical authorities is to use two complementary versions of the same worksheet, with each version reinforcing the other. This practice works best for problems than can be easily reversed. For example I could ask, "Solve the equation $x^2-2x-3=0$" and receive answers $x=3, -1.$ Conversely, I could ask, "Find a monic quadratic equation with $x=3, -1$ as roots" and receive the answer $x^2-2x-3=0$. In practice, I create two versions of the same worksheet – one version will ask the questions in the forward direction (given the equation, find the roots) and the other version will ask the questions in the reverse direction (given the roots, find the equation). When I hand out the worksheet, I give each student only one of the two versions. After ten minutes or so, students find a partner with the other version of the worksheet (color-coding helps!) and are able to check their answers. I don't need to get involved at all! This process works very well, but it does not fully resolve the issue of transferring authority to the students. In the moment, students are the authority on the correct answer to a problem. However, this authority that a certain answer is correct is still coming from me, because I supplied them with both versions of the worksheet.
My students know that if you graph the function $f(x)=A\sin (Bx+C)$ you will produce a sinusoidal wave with amplitude $|A|$, period length $2\pi\div |B|$, and a phase shift (left/right translation) of $-B/C$. Using that information, they must find parameters $A, B, \text{ and } C$ to exactly match the function below. $$y=\sin x + \cos x$$ The observant student may see that $1.414\approx \sqrt 2$ and produce the correct result $y=\sqrt 2\sin(x+\frac{\pi}{4}.$ Then students try the same approach for this next function. $$y=\sin x + 2\cos x$$ 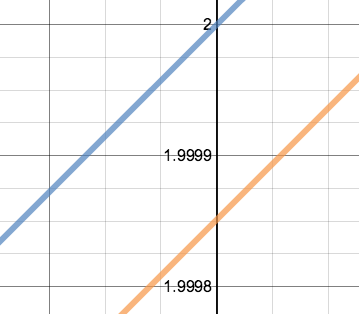 sin x + 2 cos x (blue) : √5 sin(x+1.107) (orange) sin x + 2 cos x (blue) : √5 sin(x+1.107) (orange) Again, an observant student may see that $2.236\approx \sqrt 5$ and produce $y=\sqrt 5\sin(x+1.107).$ However, if students graph the two functions and zoom in to the ten-thousandths scale, they see that the two graphs are very close but do not agree exactly. It seems that in using the number $1.107$ in our function, we have approximated to correct result but have overlooked some essential numerical relationship. We don't know where the $1.107$ came from or have an exact formula for it. Students may find it deeply unsettling to not know more about this number. When they tell me this, I tell them they have good instincts and that they should keep up the good work. |
About Me
I started this blog to share my transformation from math nerd to math nerd who loves to share math with young people. I teach high school in Hanoi, Vietnam. Your comments are always welcome. Archives
May 2021
|


 RSS Feed
RSS Feed
