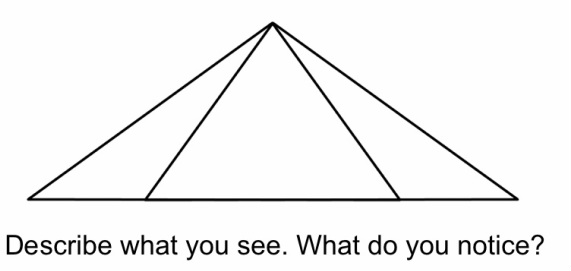
- The middle triangle looks equilateral.
- The two outside triangles are congruent.
- The two outside triangles could equal the middle triangle.
- There are a total of five vertices.
- There are two obtuse triangles on the outside.
- The angles on the base of the triangle are supplementary.
- The large triangle is isosceles.
- The baselengths of the three smallest triangles add up to the baselength of the large triangle.
- The two end triangles are scalene.
- Angles in a triangle add up to 180°.
- There are three small triangles and one large triangle.
- Actually, there are six triangles.
- The whole shape can be made from just two triangles. (Do you see it?)
- The angles of the overlapping triangles are right angles.
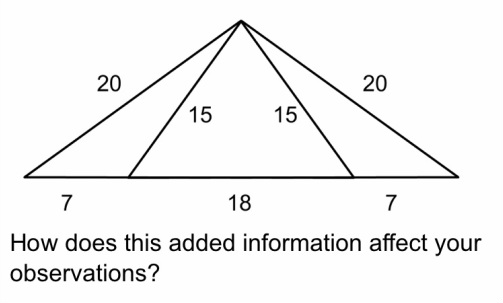
- The middle triangle looks equilateral. False.
- The two outside triangles are congruent. True, we can use Side Side Side.
- The two outside triangles could equal the middle triangle. False.
- There are a total of five vertices. True by observation.
- There are two obtuse triangles on the outside. True, we can use the converse of the Pythagorean Theorem.
- The angles on the base of the triangle are supplementary. True by linear pair.
- The large triangle is isosceles. True.
- The baselengths of the three smallest triangles add up to the baselength of the large triangle. True by observation.
- The two end triangles are scalene. True.
- Angles in a triangle add up to 180°. True always.
- There are three small triangles and one large triangle. True.
- Actually, there are six triangles. Also True.
- The whole shape can be made from just two triangles. (Do you see it?) True!
- The angles of the overlapping triangles are right angles. Awesome observation! Let's look into that!
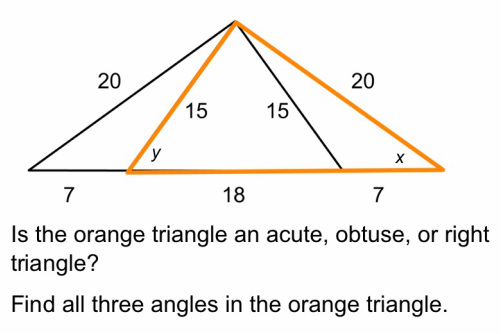
We can use the Pythagorean Theorem to see that $$15^2+20^2=(18+7)^2.$$ The orange triangle is a right triangle! Now we can use SOHCAHTOA to find the other angles! $$x=\tan ^{-1}(\frac {15}{20})=36.87\deg$$ $$y=\tan ^{-1}(\frac {20}{15})=53.13\deg.$$
Did you get all that?
 RSS Feed
RSS Feed
