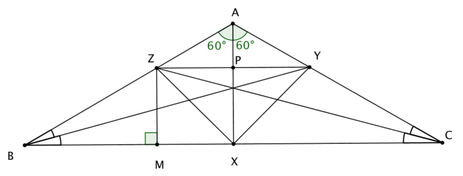
$\Delta BZM$ is a 30-60-90 triangle, so $PX = ZM = BZ / 2$, and symmetry gives $PZ = ZY / 2 = BZ / 2.$ Thus $\Delta PZX$ is an isosceles right triangle, and, similarly, so is $\Delta PYX.$ Thus the result is proved.
A place to share excitement and ideas about math education, math goings-on, and math adventures.
Read about the Big Problems course I will be teaching in the fall.
|
Recently a friend posed a Geometry problem to me: $\angle BAC = 120^{\circ}$, and $AX$ bisects $\angle BAC.$ If $BY$ and $CZ$ bisect angles $\angle ABX$ and $\angle XCA$, respectively, then $\angle ZXY$ is a right angle. After standard angle-chasing failed to produce an answer, I turned to my bag of problem solving techniques: Look at a Special Case; Investigate the Converse; and Ask a Related Question. Special Case: An easy way to simplify the problem is to assume that $\Delta ABC$ is isosceles. In this case, we can use special right triangles to prove our result.  The symmetry of $\Delta ABC$ shows that $ZY || BC \perp AX.$ Because $BY$ is an angle bisector, $\angle ZBY = \angle YBX = 15^{\circ}.$ This shows that $\Delta ZBY$ is isosceles with base $BY$. As a result, $BZ = ZY.$ $\Delta BZM$ is a 30-60-90 triangle, so $PX = ZM = BZ / 2$, and symmetry gives $PZ = ZY / 2 = BZ / 2.$ Thus $\Delta PZX$ is an isosceles right triangle, and, similarly, so is $\Delta PYX.$ Thus the result is proved. The Converse makes the right angle the assumed and attempts to prove that two segments are angle bisectors. $\angle BAC = 120^{\circ}$, and $AX$ bisects $\angle BAC.$ If $\angle ZXY$ is a right angle, then $BY$ and $CZ$ bisect angles $\angle ABX$ and $\angle XCA$, respectively. The converse is clearly proved false by the animation, because $\angle ABY$ grows and $\angle YBX$ shrinks. However, the animation lead to a related question, which I have not yet found a sufficient answer to. I am still investigating both the original and the related problems. Though I have not produced a complete answer, I do not believe I have wasted my efforts, and I've learned a lot along the way. I will take a break and return to the problem in a little while.
0 Comments
Leave a Reply. |
About Me
I started this blog to share my transformation from math nerd to math nerd who loves to share math with young people. I teach high school in Hanoi, Vietnam. Your comments are always welcome. Archives
May 2021
|