 sin x + 2 cos x (blue) : √5 sin(x+1.107) (orange)
sin x + 2 cos x (blue) : √5 sin(x+1.107) (orange) |
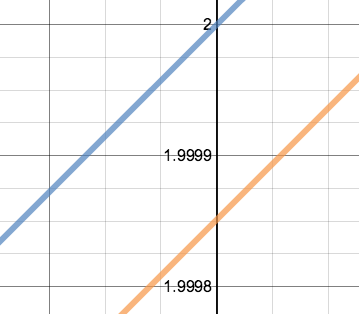
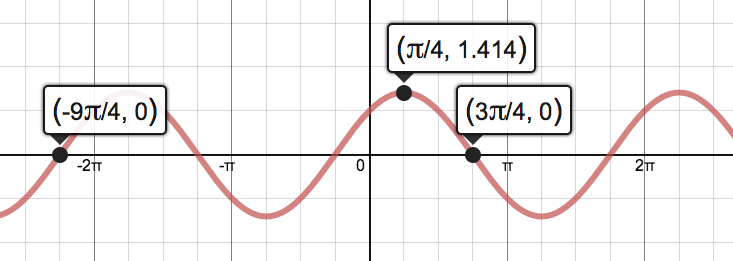
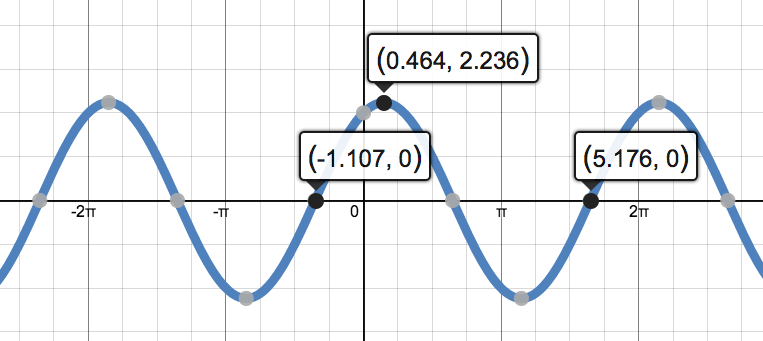
My students know that if you graph the function $f(x)=A\sin (Bx+C)$ you will produce a sinusoidal wave with amplitude $|A|$, period length $2\pi\div |B|$, and a phase shift (left/right translation) of $-B/C$. Using that information, they must find parameters $A, B, \text{ and } C$ to exactly match the function below. $$y=\sin x + \cos x$$ The observant student may see that $1.414\approx \sqrt 2$ and produce the correct result $y=\sqrt 2\sin(x+\frac{\pi}{4}.$ Then students try the same approach for this next function. $$y=\sin x + 2\cos x$$  sin x + 2 cos x (blue) : √5 sin(x+1.107) (orange) sin x + 2 cos x (blue) : √5 sin(x+1.107) (orange) Again, an observant student may see that $2.236\approx \sqrt 5$ and produce $y=\sqrt 5\sin(x+1.107).$ However, if students graph the two functions and zoom in to the ten-thousandths scale, they see that the two graphs are very close but do not agree exactly. It seems that in using the number $1.107$ in our function, we have approximated to correct result but have overlooked some essential numerical relationship. We don't know where the $1.107$ came from or have an exact formula for it. Students may find it deeply unsettling to not know more about this number. When they tell me this, I tell them they have good instincts and that they should keep up the good work.
0 Comments
Leave a Reply. |
About Me
I started this blog to share my transformation from math nerd to math nerd who loves to share math with young people. I teach high school in Hanoi, Vietnam. Your comments are always welcome. Archives
May 2021
|
 RSS Feed
RSS Feed
