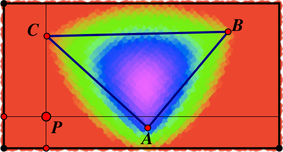
- What shape do the contours of the same color make?
- What is the point at the "center" of the triangle has the deepest shade of violet?
- Each contour is a convex figure.
- A contour may enclose zero, one, two, or three of the foci. Note that this is in contrast to the case of a circle or an ellipse.
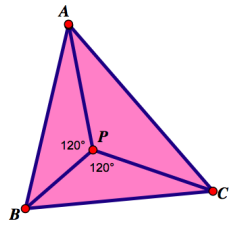
Case 2: The three foci form a triangle $\Delta ABC$ one of whose angles measures greater than $120^{\circ}.$ In this case, the point $P$ is located at the vertex of this largest angle.
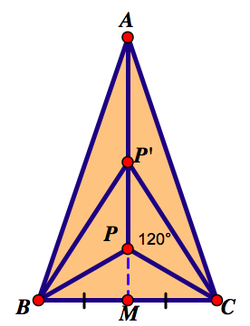 Figure 2
Figure 2 To aid our proof, we note that minimizing $AP' + BP' + CP'$ is equivalent to minimizing $BP' + CP' - P'M$ and divide our proof into two cases.
Let $x=PM, x\sqrt{3} = BM = CM, 2x=PB = PC.$ In addition, let $y=BP' = CP'$ and $z=PP'.$
Case 1: $P'$ is above $P.$ To show our point, we need to show that $3x < 2y-x-z,$ which is equivalent to $z < 2y - 4x.$
By the Pythagorean Theorem, $z=\sqrt{y^2-3x^2}-x.$ We show the result by reversing the steps of
$$\sqrt{y^2-3x^2}-x<2y-4x$$
$$\sqrt{y^2-3x^2}<2y-3x$$
$$y^2-3x^2<4y^2-12xy+9x^2$$
$$0<3y^2-12xy+12x^2$$
$$0<3(y-2x)^2,$$
which is certainly true, because $2y-3x$ is positive.
- Can I provide a description of the shape of the contours generated by three foci?
- Can I prove that contours are always convex?
- Can I complete the above proof for non-isosceles triangles?
- I was able to provide a simple description of the tri-center in terms of the 120°-point of a triangle. Does this generalize easily to the case with four or more foci?
- How can one construct the 120°-point of a given triangle?
 RSS Feed
RSS Feed
