
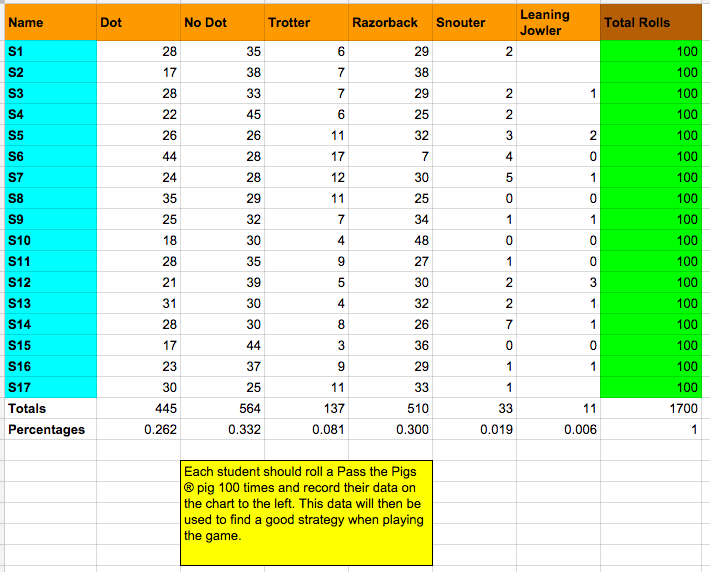
In our Discrete Math class, we analyzed this game mathematically. There are six possible ways for one pig to land when it is rolled, creating thirty-six possible ways for two pigs to land. Each of these thirty-six possible ways has an associated point value, and the Pig Out causes you to lose all your points for the round. Our class collectively rolled a single die 1,700 times to find the probability of each outcome. We decided we should continue to roll as long as our expected value gained was larger than our expected loss, summarized as $$EV>EL$$ where $EV$ is the expected value of rolling two pigs and $EL$ is our expected loss if we roll a Pig Out.
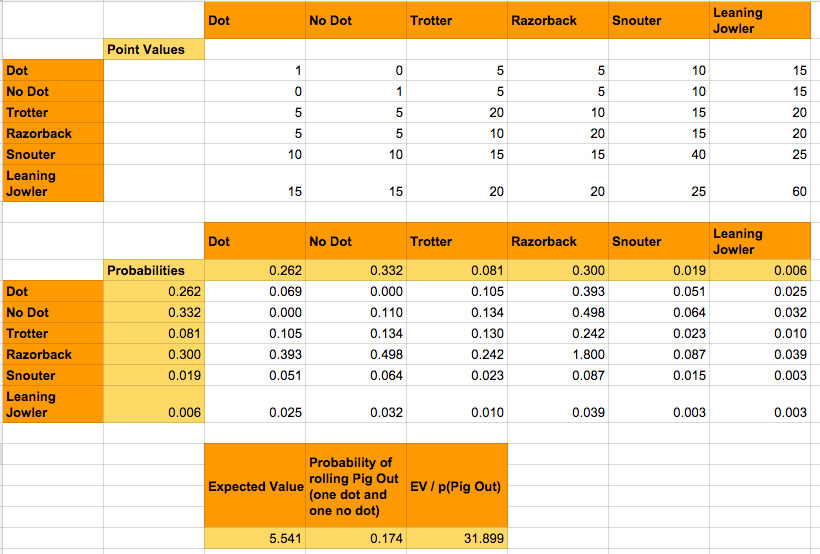
In our situation $EV$ can be found by multiplying the point value of each of the 36 possible outcomes by its probability of occurring and adding the values together. $EL$ can be found by multiplying the probability of a Pig Out by the number on points you stand to lose: $EL=p(\text{Pig Out})n$. Based on our calculations (see below) we found $$5.541>0.174 n,$$ or $$n<31.9.$$
This tells us that we should continue to roll as long as we have 31 or fewer points for a round.
For those interested in the details of our calculations, please read the more technical description below.
 RSS Feed
RSS Feed
