- Any letter can turn into an A.
- Two C’s in a row can turn into a B.
- Any word can be doubled, i.e. placed after itself.
- Add two C's to a word.
- Any C can turn into three C's.
- Triple the beginning letter of a word.
How do we know what Rule 4 actually is?
We need more data to test our three hypotheses!


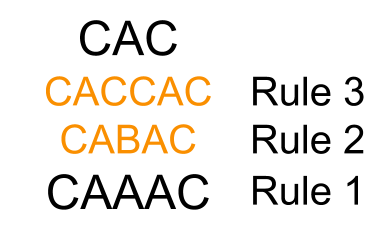

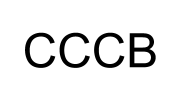
 RSS Feed
RSS Feed
