|
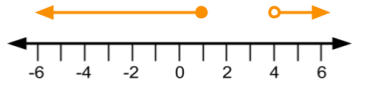
I had more trouble with a recent in-class activity than I had anticipated. Students were given cards with simple inequalities and asked to form groups of 3 around a joining conjunction "AND" or "OR" and graph the compounded, resulting inequality.  Students were quite comfortable graphing the compound inequality above. The two arms point outwards from 1 and 4, respectively. However, when asked to graph an inequality where both arms pointed in the same direction, the students had much greater difficulty. For example, students had trouble viewing the inequality $x >0 \text{ AND } x>3$ as equivalent to $x>3.$ To get to the bottom of the misunderstanding, I decided to ask students their thoughts about how AND and OR graphs work. Students responded that an OR graph has "two parts" and a "gap in between," while an AND graph has "one part" and "no gap." I realized that students' experience of AND and OR graphs had only been in the context of absolute value inequalities, where these descriptions are (almost) always true. However, if given a compound inequality that does not come from an absolute value, these descriptions may not apply. I needed to find a way to show my students a more inclusive description of compound inequalities. At this point, as if prompted, another student, gave another description of an AND graph as "two graphs overlap" and an OR graph as "any two lines — doesn't matter if they intersect." While the wording could use some work, the idea is there that AND means to take the two graphs' intersection and OR to take their union. We wrote both student-given descriptions of AND and OR graphs on the board in an attempt to judge between them. When the bell rang I had to let students go. It was worth it to spend class time in discussion, even if I didn't get to everything I had planned. We'll just have to pick up on these ideas next week.
0 Comments
Leave a Reply. |
About Me
I started this blog to share my transformation from math nerd to math nerd who loves to share math with young people. I teach high school in Hanoi, Vietnam. Your comments are always welcome. Archives
May 2021
|
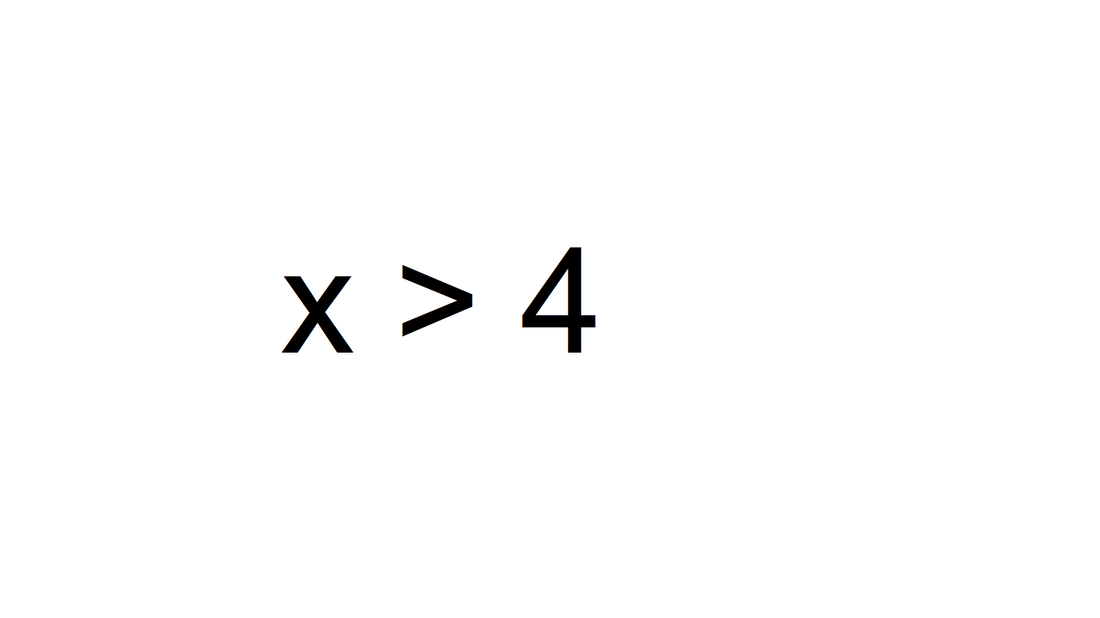

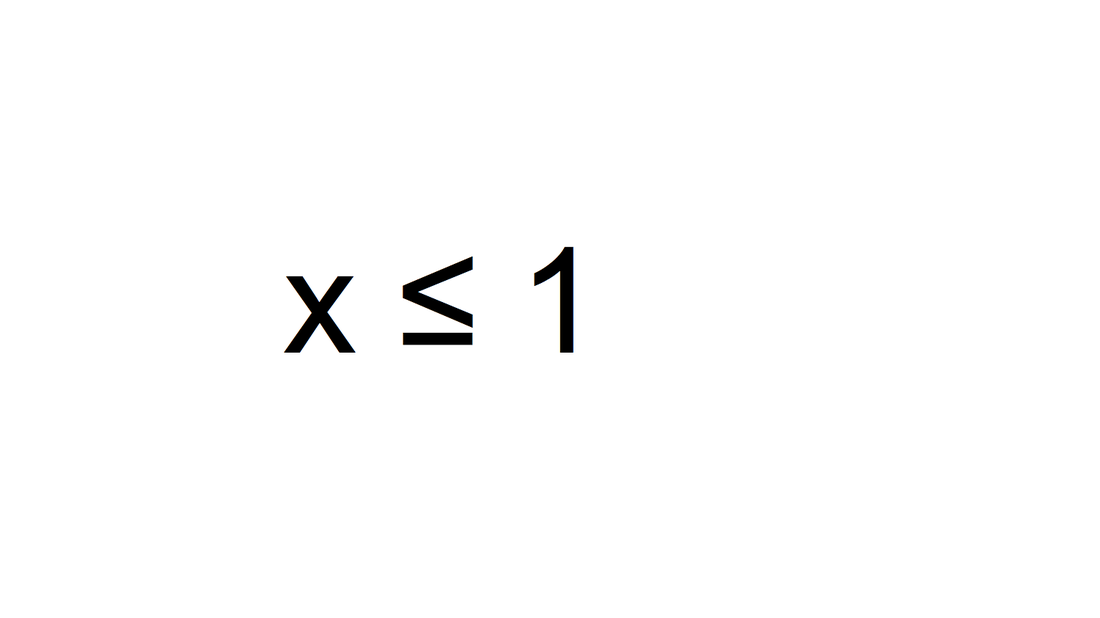
 RSS Feed
RSS Feed
