|
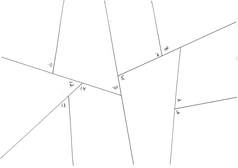
When working a mathematical problem, there are many sources of authority a pupil can reference to check the accuracy of their work: As a teacher, I am in the business of developing Independent Problem Solvers. In practice, I nudge students away from the first two sources of authority towards the second two. There is, however, one more authority that I have not mentioned. This final authority is the basis of any scientific journal: the consensus of one's peers. Students can access the authority of their peers when they are forced to discuss their answers with their classmates.  Practically, I assign several book problems during class and tell students to work independently. After five to ten minutes, I interrupt the class. I tell them that they will have to combine all of their answers onto a single sheet that they will turn in. Each group is given a large sheet of paper already sectioned-off and numbered. There is one region for each of the assigned book problems. It is the groups' responsibility to agree on which work and answer to put on the one sheet they submit together. The combined pressures of needing to submit their work and to work together gets the students arguing about the correct solution to each problem - exactly what I want.
0 Comments
We spent several days in class discussing Pythagorean Triples. These are whole number solutions to the Pythagorean Theorem: if $a$ and $b$ are the legs of a right triangle and $c$ is its hypotenuse, then $a^2 + b^2 = c^2." In class, we discussed two patterns that can help us find Pythagorean Triples. 1. Any scale multiple of a Pythagorean Triple is also a Pythagorean Triple. For example $3, 4, 5$ is a Pythagorean Triple, and so are $6, 8, 10;$ $9, 12, 15;$ and $3k, 4k, 5k$ for any whole number $k.$ 2. If we look at the Pythagorean Triples where $c$ is two greater than $b,$ the differences between successive values of $b$ and $c$ display linear growth as you can see in the examples below. From the first line to the second, $b$ and $c$ both increase by $7.$ From the second line to the third, $b$ and $c$ both increase by $9.$ From the third line to the fourth, $b$ and $c$ both increase by $11.$ This difference continues to increase by $2$ between each two lines. On the most recent quiz, I gave two extra credit questions asking students to find Pythagorean Triples under certain parameters. Students used both of the above techniques, and one industrious student employed her own approach to find a solution to $22^2 + b^2 = c^2,$ where $b+2 = c$: 3. Substitute $b+2$ for $c$ and use algebra Bravo.
|
About Me
I started this blog to share my transformation from math nerd to math nerd who loves to share math with young people. I teach high school in Hanoi, Vietnam. Your comments are always welcome. Archives
May 2021
|

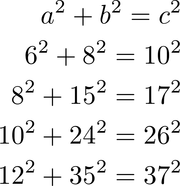
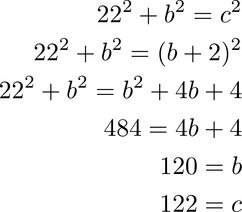
 RSS Feed
RSS Feed
