|
The video provides you with constant information about the car's speed and time. That is enough information to closely approximate the total distance of one lap around the track. After we calculate the distance around the track, we can look up the actual length of the track to see how close our approximation is! I turned this idea into a project for my AP Calc class. Enjoy!
0 Comments
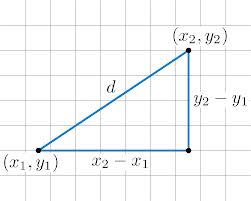
I've been thinking about how to help my students see the distinction between what they know through reason and what they know by intuition. I devised a situation where their intuition won't help them at all, because I made it up myself. The scenario is below. I'll report back how they respond. It was ten minutes until I had to teach my ninth grade class, and I’d worked hard to get this lesson right. The textbook’s next section was all about measuring the distance between any two points in the plane using the distance formula. The formula was second nature to me, but I knew that the students would have trouble remembering and using it correctly. At its simplest, the distance formula is the Pythagorean Theorem in a new environment. Most students were familiar with the formula $a^2 + b^2 = c^2$ and how to use it. The main focus of my lesson was to use their previous experience to tell a story about applying old knowledge to new situations.
With only a few minutes to go before my class came in, in addition to weaving my tale of a distance formula - Pythagorean Theorem analogy, I had a list of technical bullet points that I had to mention. I had seen students get stuck on these details, and to keep the lesson going smoothly, I wanted to short-circuit any misunderstandings. As I was feeling anxious that I might forget one of my talking points, I realized that the advice I was giving my students was exactly the advice I needed to hear myself. Taken separately, any list is difficult and cumbersome to memorize, but lists become easy when they tell a story or help jog a strong memory. No one can remember a jumble of mathematical symbols, but each part of the distance formula tells part of the story of using the Pythagorean Theorem: we subtract the x-coordinates and the y-coordinates – that’s measuring the legs of our right triangle; we square each of these numbers and add the results – that’s using the Pythagorean Theorem; finally, we square root the answer – that’s just putting the last step of using the Pythagorean Theorem, finding c, into the formula. This is the clarity and direction that I hope to bring to my lessons.  My students are very good at spotting falsehoods. An if-then statement can be either true or false, as can its converse. For example,
Another student came up with
These students have their priorities straight:) |
About Me
I started this blog to share my transformation from math nerd to math nerd who loves to share math with young people. I teach high school in Hanoi, Vietnam. Your comments are always welcome. Archives
May 2021
|
 RSS Feed
RSS Feed
