
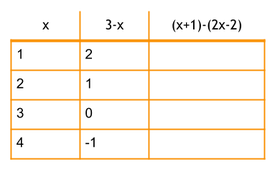
• Imprecise – "Plug in your solution into both sides of the equation and see if it works out."
• Narrowly Applicable – "Plug in -6 into both sides of the equation and see that you get -19 on both sides."
• Precise and Broadly Applicable – "You can plug your answer into both expressions. If you get the same answer, the number you found is correct."
This last answer clearly tell you what to do – plug your answer into both sides of the equation and check if the values are the same – and applies to any equation.
There are two appealing consequences of my new verbal aptitude. The first benefit is pedagogical. Because I have tools to discern among good and bad student responses, I am able to hold them to a higher standard in their writing. The second benefit is aesthetic. The two conditions of precision and broad applicability are dual qualities in much the same way that we insist on linear independence and spanning properties for the basis of a vector space. This might be a case of pedagogy imitating math.
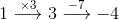

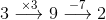
 RSS Feed
RSS Feed
