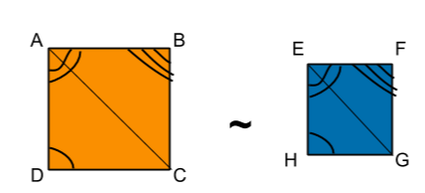
| Argument 1 Yes, the two shapes must be similar. If you draw segments $AC$ and $EG$, then you have two pairs of similar triangles. $\angle A \approx \angle E$ and $\angle D \approx \angle H$ so $\Delta ACD \sim \Delta EGH.$ Similarly $\Delta ACB \sim \Delta EGF.$ Because their two constituent triangles are similar, we must have $ABCD \sim EFGH.$ | Argument 2 No, it is possible the shapes are not similar. Consider the example above of two rectangles. All their angles are congruent, but the shapes are clearly not similar. |
|
I had just introduced the class to the AA Similarity Postulate - the idea that if triangles have two pairs of congruent angles, then one is a scaled-up version of the other, i.e. they are similar. I posed my class the following question. Is there a corresponding AAA Similarity Theorem for quadrilaterals? I was impressed by how clearly my students argued two different views on the question. Who do you believe?
2 Comments
Bill Coley
2/2/2017 08:34:35 am
Math is not my strong point but it looks like argument 2 is clearly correct.
Reply
Leave a Reply. |
About Me
I started this blog to share my transformation from math nerd to math nerd who loves to share math with young people. I teach high school in Hanoi, Vietnam. Your comments are always welcome. Archives
May 2021
|

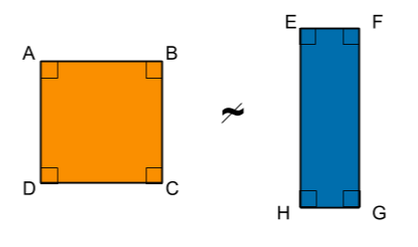
 RSS Feed
RSS Feed
